![ДИФФЕРЕНЦИАЦИЯ ЗВУКОВ [С – Ш] - Научно-практический Центр \"ЗДОРОВЬЕ НАЦИИ\" ДИФФЕРЕНЦИАЦИЯ ЗВУКОВ [С – Ш] - Научно-практический Центр \"ЗДОРОВЬЕ НАЦИИ\"](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-0.webp)




![Дифференциация звуков [с]-[ш] - YouTube Дифференциация звуков [с]-[ш] - YouTube](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-7.webp)
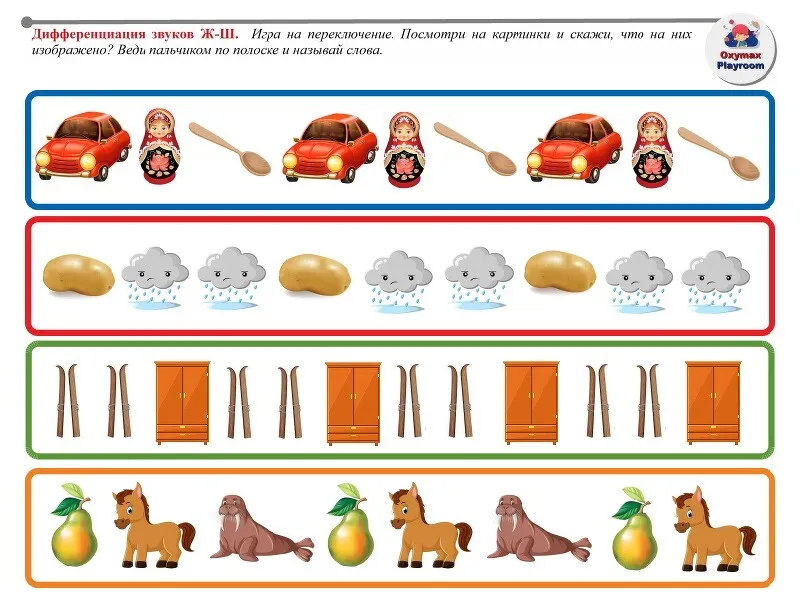

![Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] Татьяна Березенкова - купить книгу Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] в Минске — Издательство Учитель на OZ.by Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] Татьяна Березенкова - купить книгу Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] в Минске — Издательство Учитель на OZ.by](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-10.webp)

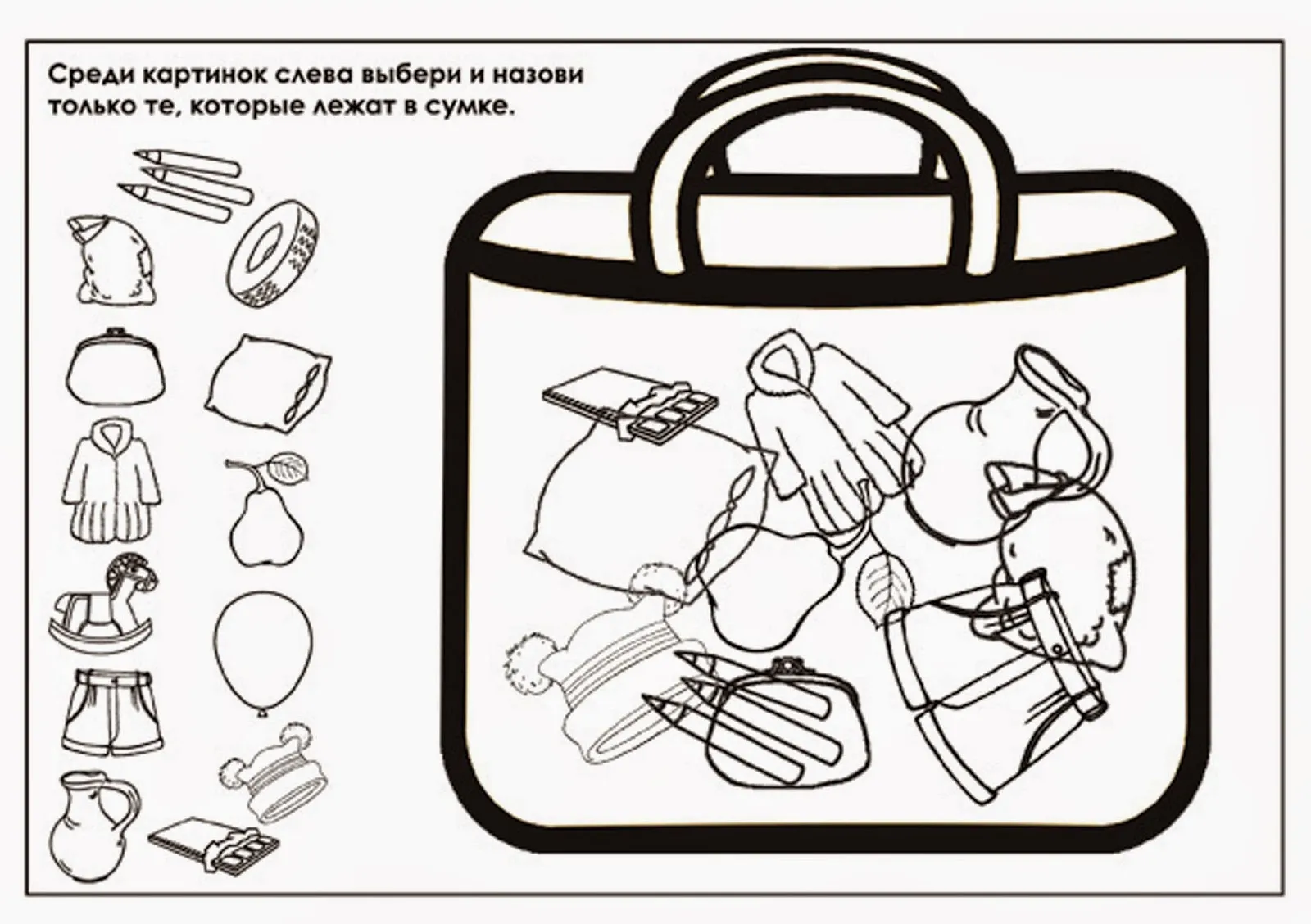

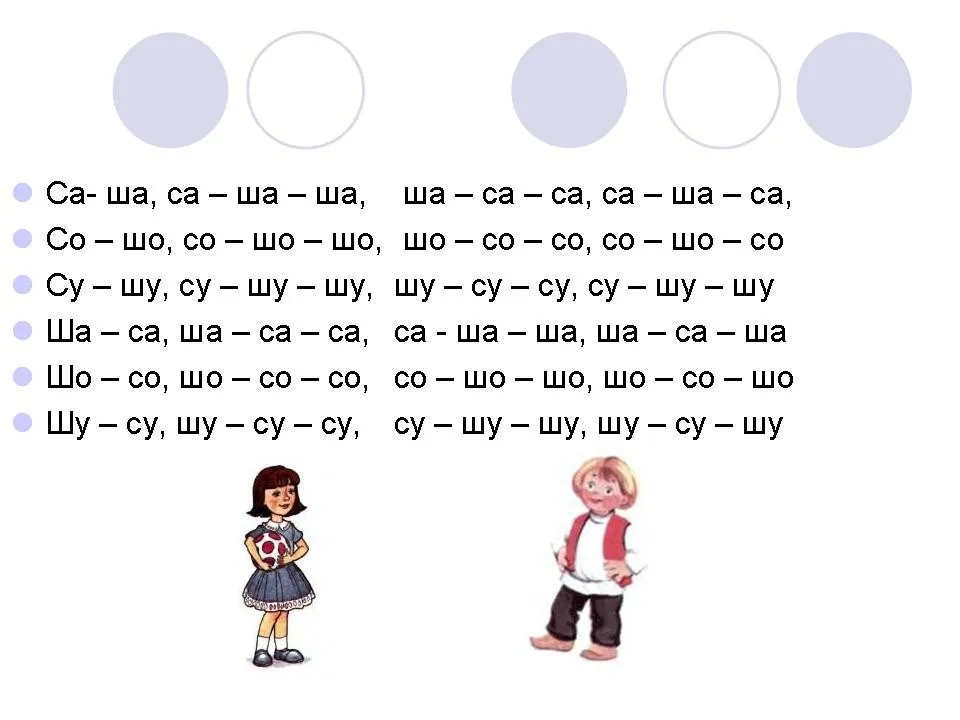
![Индивидуально подгрупповое занятие \"Дифференциация звуков [c]–[ш] в слогах и словах\" Индивидуально подгрупповое занятие \"Дифференциация звуков [c]–[ш] в слогах и словах\"](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-15.webp)
![Дидактическая игра «Два — пять» по дифференциации звуков [Ш]-[Ж]-[Р]-[Р'] (1 фото). Воспитателям детских садов, школьным учителям и педагогам - Маам.ру Дидактическая игра «Два — пять» по дифференциации звуков [Ш]-[Ж]-[Р]-[Р'] (1 фото). Воспитателям детских садов, школьным учителям и педагогам - Маам.ру](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-16.webp)


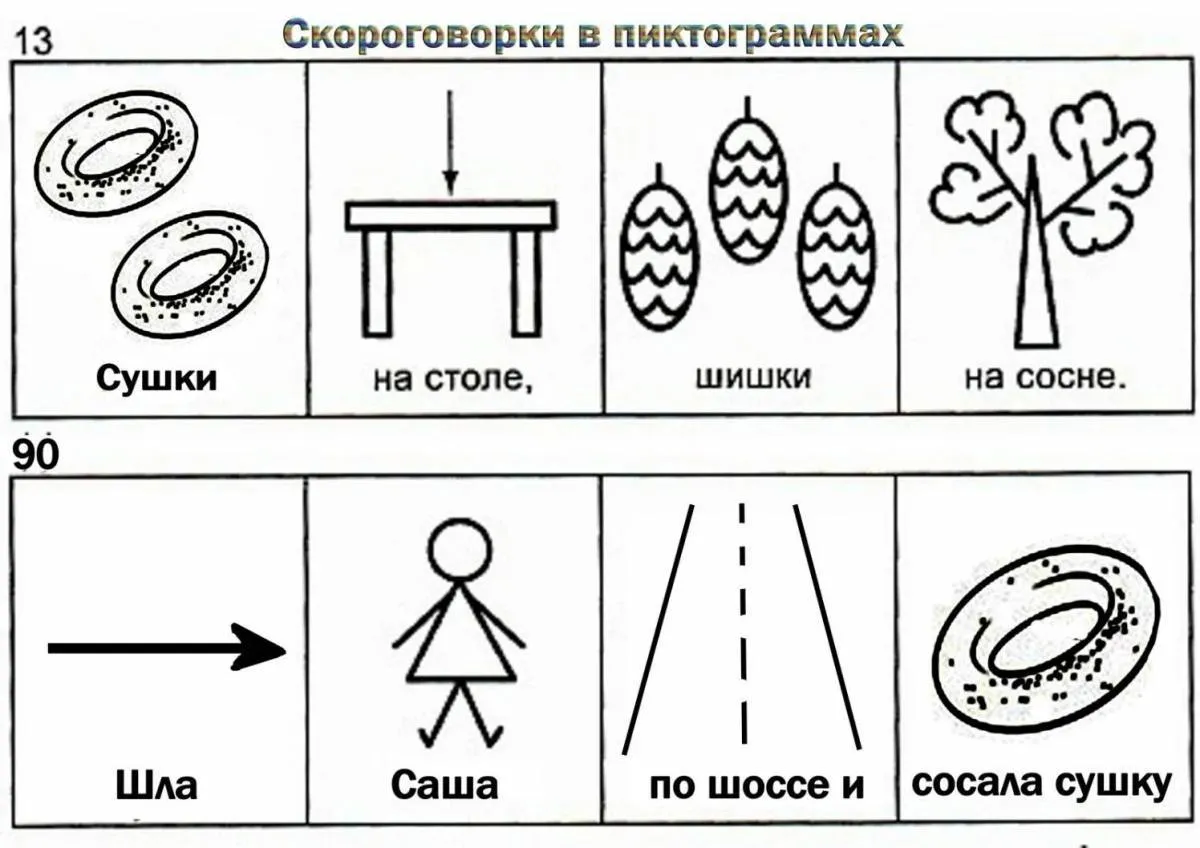






![Логопедическая игра «Сова Соня и мишка Шалун собирают игрушки» по дифференциации звуков [с]-[ш] в словах (8 фото). Воспитателям детских садов, школьным учителям и педагогам - Маам.ру Логопедическая игра «Сова Соня и мишка Шалун собирают игрушки» по дифференциации звуков [с]-[ш] в словах (8 фото). Воспитателям детских садов, школьным учителям и педагогам - Маам.ру](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-26.webp)
![Найди отличия. Выпуск 4. Дифференциация звуков [с]-[ш], [з]-[ж], [р]-[р?]-[л]-[л?] в словах и предложениях.ФГОС, Бухарина К.Е. , Детство-пресс , 9785907317239 2020г. 186,50р. Найди отличия. Выпуск 4. Дифференциация звуков [с]-[ш], [з]-[ж], [р]-[р?]-[л]-[л?] в словах и предложениях.ФГОС, Бухарина К.Е. , Детство-пресс , 9785907317239 2020г. 186,50р.](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-27.webp)
![Дифференциация звуков [ш–ж] в слогах, словах Дифференциация звуков [ш–ж] в слогах, словах](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-28.webp)








![Иллюстрация 1 из 6 для Автоматизация и дифференциация звуков в рассказах. Выпуск 2. Звуки [ш], [ж], [с], [с'], [ц], [ч] - Наталия Нищева | Лабиринт - книги. Источник: Лабиринт Иллюстрация 1 из 6 для Автоматизация и дифференциация звуков в рассказах. Выпуск 2. Звуки [ш], [ж], [с], [с'], [ц], [ч] - Наталия Нищева | Лабиринт - книги. Источник: Лабиринт](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-38.webp)





![Автоматизация и дифференциация звуков в рассказах. Выпуск 2. Звуки [ш], [ж], [с], [с'], [ц]. Нищева Н. В. (5517730) - Купить по цене от 139.00 руб. | Интернет магазин SIMA-LAND.RU Автоматизация и дифференциация звуков в рассказах. Выпуск 2. Звуки [ш], [ж], [с], [с'], [ц]. Нищева Н. В. (5517730) - Купить по цене от 139.00 руб. | Интернет магазин SIMA-LAND.RU](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-45.webp)

![Дифференциация звуков [С-Ш] - Сапрыгина Елена - скачать на Wildberries Цифровой | 130745 Дифференциация звуков [С-Ш] - Сапрыгина Елена - скачать на Wildberries Цифровой | 130745](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-47.webp)
![Порычим-полалакаем. Дифференциация звуков [Р], [Р'], [Л], [Л'] – купить по цене: 46,80 руб. в интернет-магазине УчМаг Порычим-полалакаем. Дифференциация звуков [Р], [Р'], [Л], [Л'] – купить по цене: 46,80 руб. в интернет-магазине УчМаг](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-51.webp)


![НейроЛОГОраскраска. Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] - купить книгу с доставкой в интернет-магазине «Читай-город». НейроЛОГОраскраска. Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] - купить книгу с доставкой в интернет-магазине «Читай-город».](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-55.webp)
![Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск 2. Нищева Н. В. (5522830) - Купить по цене от 131.00 руб. | Интернет магазин SIMA-LAND.RU Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск 2. Нищева Н. В. (5522830) - Купить по цене от 131.00 руб. | Интернет магазин SIMA-LAND.RU](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-56.webp)
![НейроЛОГОраскраска. Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] 410240 Издательство Учитель - купить оптом от 35,50 рублей | Урал Тойз НейроЛОГОраскраска. Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] 410240 Издательство Учитель - купить оптом от 35,50 рублей | Урал Тойз](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-57.webp)
![Комарова Л.А. Автоматизация звука [Ш] в игровых упражнениях: альбом дошкольника - купить в LogopedKniga.ru Комарова Л.А. Автоматизация звука [Ш] в игровых упражнениях: альбом дошкольника - купить в LogopedKniga.ru](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-58.webp)


![Тексты и картинки для автоматизации и дифференциации звуков [л], [л'], [р], [р']: Выпуск 4, Нищева Наталья Валентиновна . Кабинет логопеда , Детство-пресс , 9785907009073 2023г. 183,00р. Тексты и картинки для автоматизации и дифференциации звуков [л], [л'], [р], [р']: Выпуск 4, Нищева Наталья Валентиновна . Кабинет логопеда , Детство-пресс , 9785907009073 2023г. 183,00р.](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-61.webp)




![Автоматизация и дифференциация звуков в рассказах. Выпуск 2. Звуки [ш], [ж], [с], [с'], [ц], [ч], [т']. С 5 до 7 лет – Книжный интернет-магазин Kniga.lv Polaris Автоматизация и дифференциация звуков в рассказах. Выпуск 2. Звуки [ш], [ж], [с], [с'], [ц], [ч], [т']. С 5 до 7 лет – Книжный интернет-магазин Kniga.lv Polaris](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-68.webp)


![Электронный образовательный ресурс «Учимся говорить и различать звуки [c], [ ш] и буквы С, Ш» – NG-PRESS.BY Электронный образовательный ресурс «Учимся говорить и различать звуки [c], [ ш] и буквы С, Ш» – NG-PRESS.BY](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-73.webp)
![Звуки [С] - [Ш]. Дифференциация звуков - Лучшее. Воспитателям детских садов, школьным учителям и педагогам - Маам.ру Звуки [С] - [Ш]. Дифференциация звуков - Лучшее. Воспитателям детских садов, школьным учителям и педагогам - Маам.ру](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-74.webp)



![Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск 2. Нищева Н. В. цена, купить Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск 2. Нищева Н. В. цена, купить Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-78.webp)

![НейроЛОГОраскраска. Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] - купить книгу с доставкой в интернет-магазине «Читай-город». НейроЛОГОраскраска. Пожужжим-пошипим. Дифференциация звуков [Ж], [Ш] - купить книгу с доставкой в интернет-магазине «Читай-город».](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-82.webp)

![Книга Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск 2.ФГОС • Нищева Н.В. - купить по цене 150 руб. в интернет-магазине Inet-kniga.ru | ISBN 978-5-90693-799-5 Книга Тексты и картинки для автоматизации и дифференциации звуков [С], [З], [Ш], [Ж]. Выпуск 2.ФГОС • Нищева Н.В. - купить по цене 150 руб. в интернет-магазине Inet-kniga.ru | ISBN 978-5-90693-799-5](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-84.webp)
![Побубним-попыхтим. Автоматизация и дифференциация звуков [Б], [Б'], [П], [П'] – купить по цене: 46,80 руб. в интернет-магазине УчМаг Побубним-попыхтим. Автоматизация и дифференциация звуков [Б], [Б'], [П], [П'] – купить по цене: 46,80 руб. в интернет-магазине УчМаг](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-85.webp)
![Издательство \"Детство-Пресс\" | Автоматизация и дифференциация звуков в рассказах. Выпуск 3. Звуки [л], [л'], [р], [р'], [j] с 5 до 7 лет: Учебно-методическое пособие. (Кабинет логопеда). ФГОС Издательство \"Детство-Пресс\" | Автоматизация и дифференциация звуков в рассказах. Выпуск 3. Звуки [л], [л'], [р], [р'], [j] с 5 до 7 лет: Учебно-методическое пособие. (Кабинет логопеда). ФГОС](/files/img/photo/differentsiatsiia-s-sh-v-kartinkakh/differentsiatsiia-s-sh-v-kartinkakh-88.webp)

Дифференциация является важной математической операцией, используемой для вычисления производной функции. Она позволяет нам определить, как функция меняется при изменении ее входных параметров. В этой статье мы рассмотрим дифференциацию с шагом, а также разберем ее визуальное представление с помощью картинок.
Что такое дифференциация с шагом?
Дифференциация с шагом, также известная как численное дифференцирование, является одним из методов приближенного вычисления производной функции. Она основана на идее разделения изменения функции на маленькие шаги и вычисления приближенного значения производной на каждом из этих шагов.
Пример численной дифференциации
Давайте рассмотрим пример функции f(x) = x^2 и попробуем вычислить ее производную с помощью численной дифференциации. Для этого мы выберем некоторый маленький шаг h и используем следующую формулу:
f'(x) ≈ (f(x + h) - f(x)) / h
Где f'(x) - приближенное значение производной функции f(x) в точке x.
Для определения значения производной в каждой точке, мы выберем несколько значений h и вычислим приближенное значение производной для каждого из них. Затем мы построим график, чтобы визуально представить изменение производной в зависимости от выбранного значения шага.
Визуализация дифференциации с шагом
Ниже представлен график, на котором показано изменение производной функции f(x) = x^2 при различных значениях шага h:
- При
h = 0.1, мы видим, что значение производной постепенно уменьшается с увеличениемx, но остается положительным. - При
h = 0.01, мы замечаем, что значение производной более точно приближается к истинному значению производной, так как шаг становится еще меньше. - При
h = 0.001, мы видим, что значение производной близко к нулю в большей части области, за исключением окрестности точкиx = 0, где значение производной равно нулю.
Таким образом, мы можем наблюдать, как изменение значения шага h влияет на точность вычисления производной функции.
Заключение
Дифференциация с шагом - это метод численного вычисления производной функции. Мы использовали функцию f(x) = x^2 как пример и визуализировали изменение производной при различных значениях шага h. Чем меньше значение шага, тем более точное приближение мы получаем. Этот метод полезен в случаях, когда аналитическое вычисление производной затруднительно или невозможно.
Надеюсь, эта статья помогла вам лучше понять дифференциацию с шагом и ее визуальное представление с помощью картинок.

