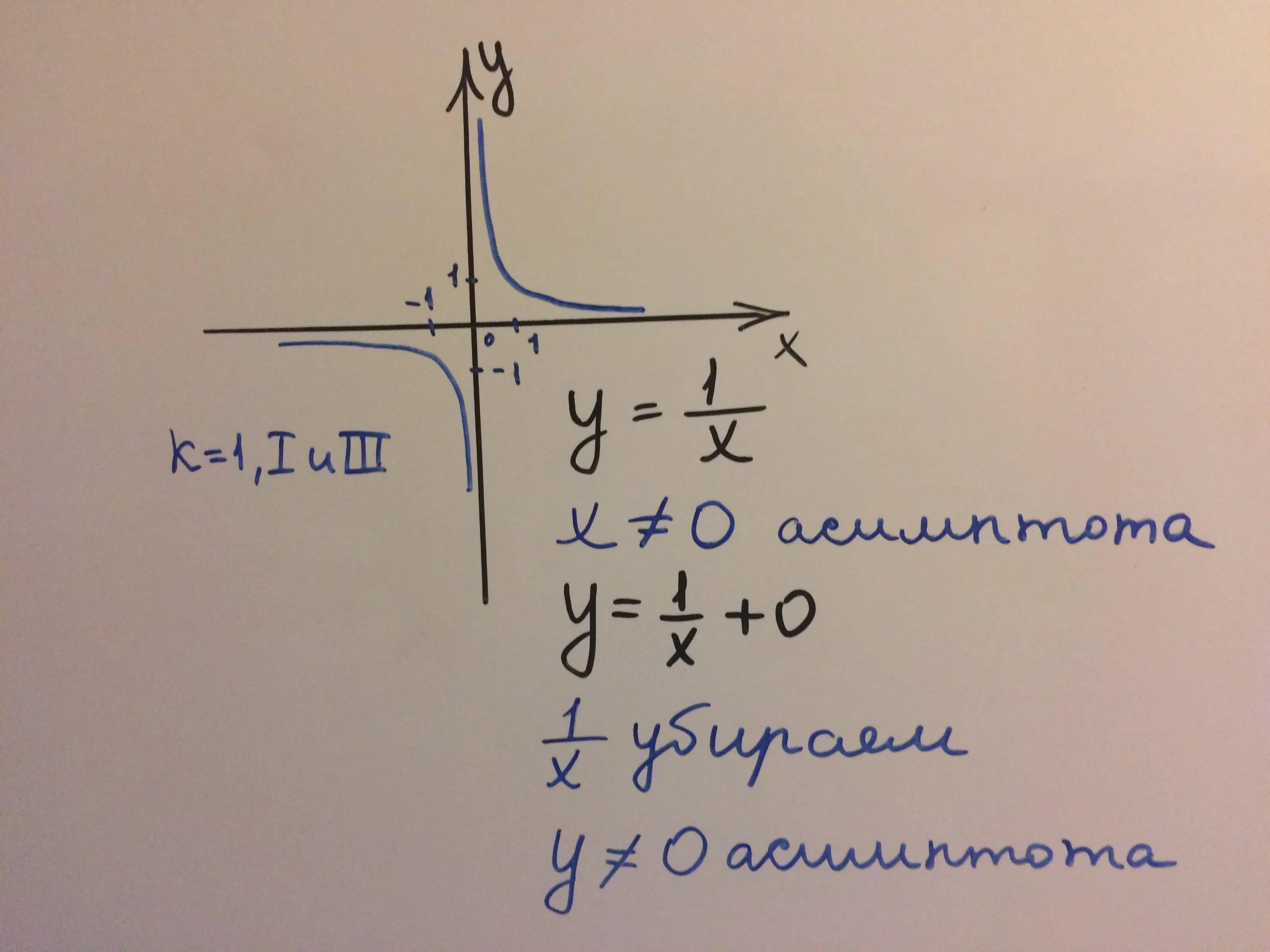
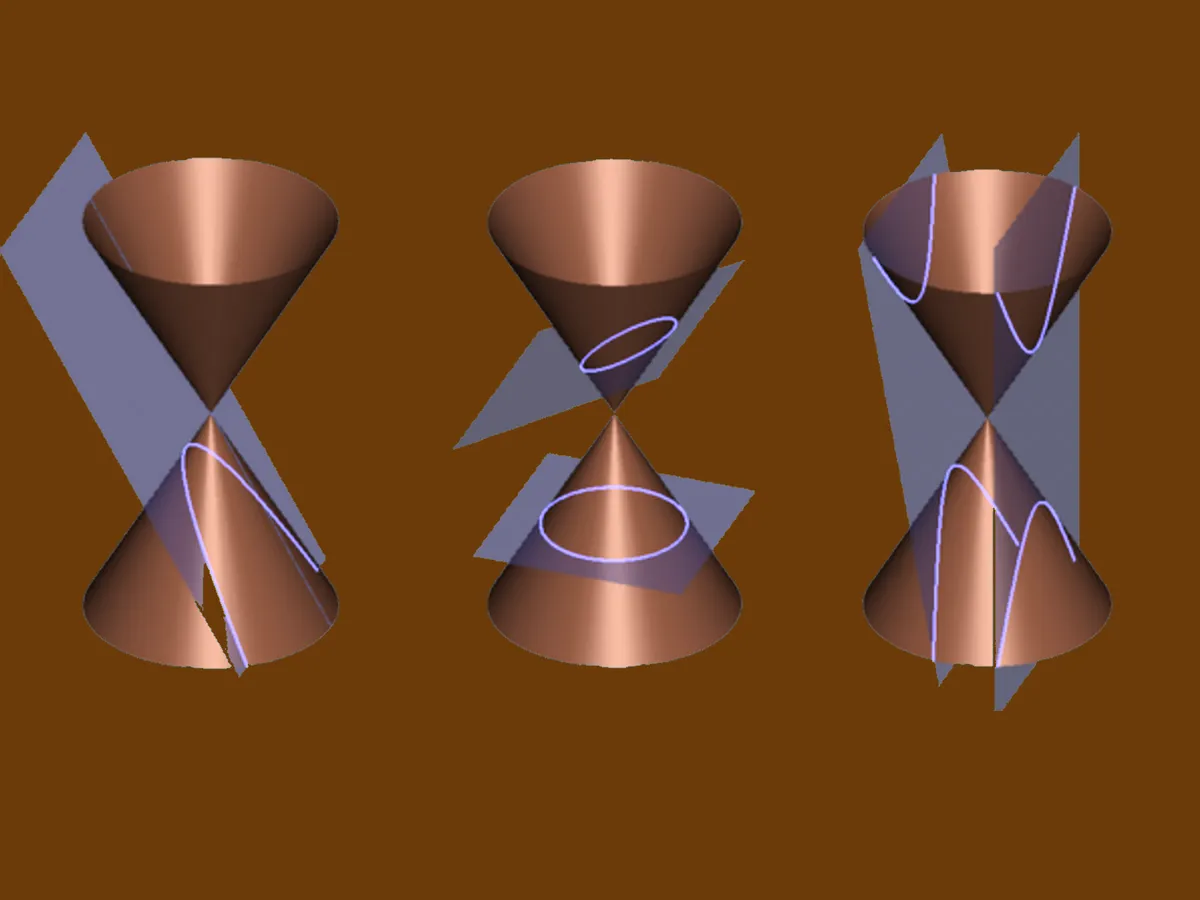







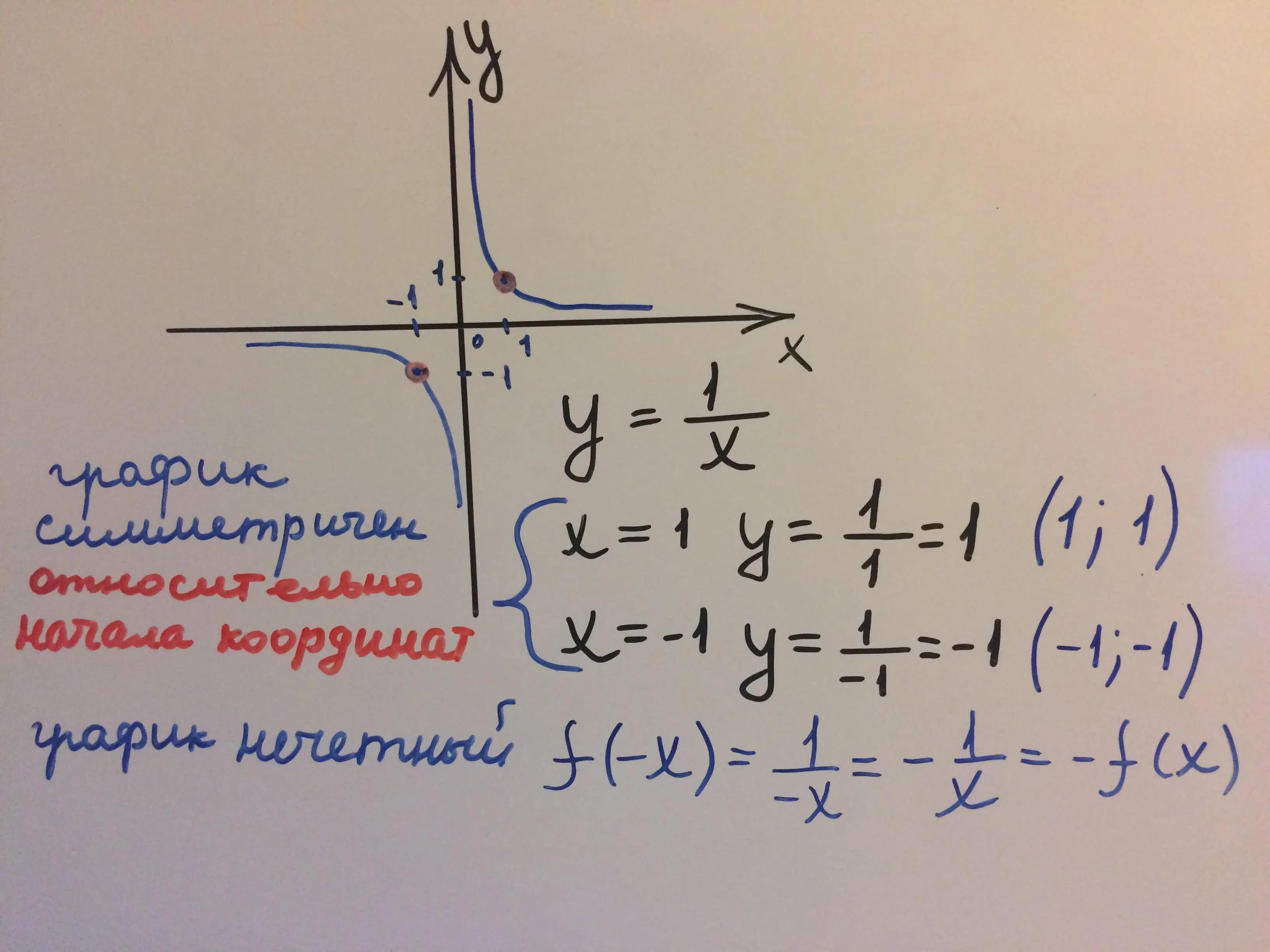




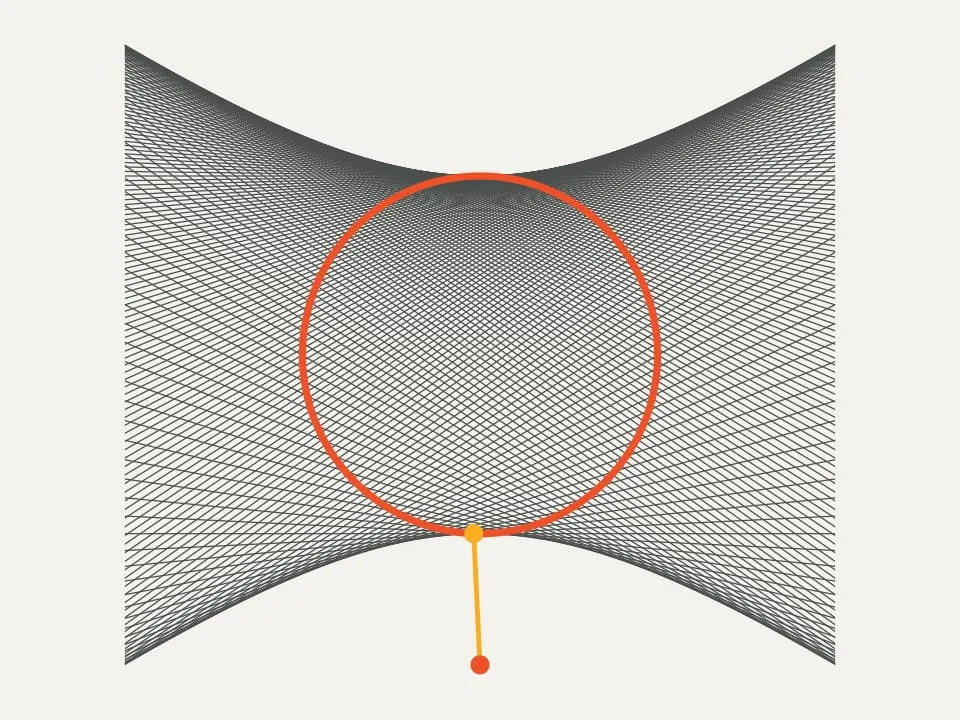
















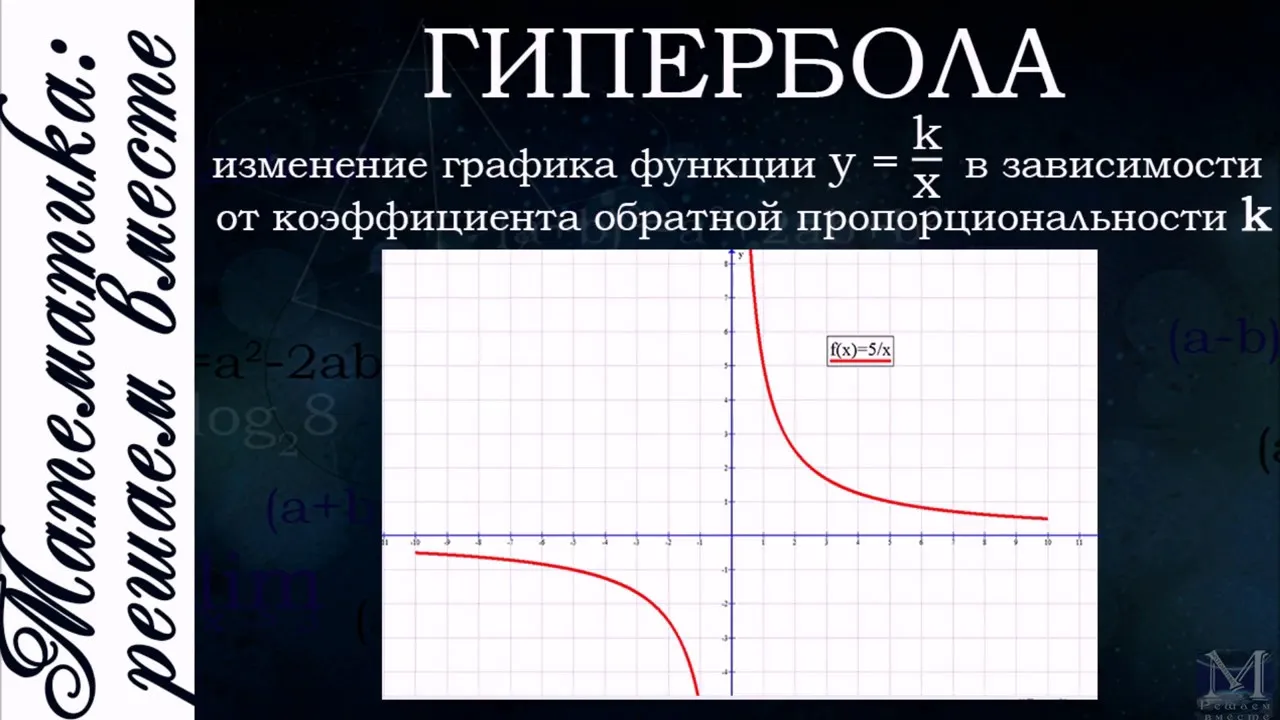



























Гипербола - это одно из классических геометрических тел, которое широко применяется в математике и физике. Гипербола имеет своеобразную форму, которая выглядит как две ветви, которые расходятся в бесконечность. В этой статье мы рассмотрим основные характеристики гиперболы и ее применение в различных областях.
Определение гиперболы
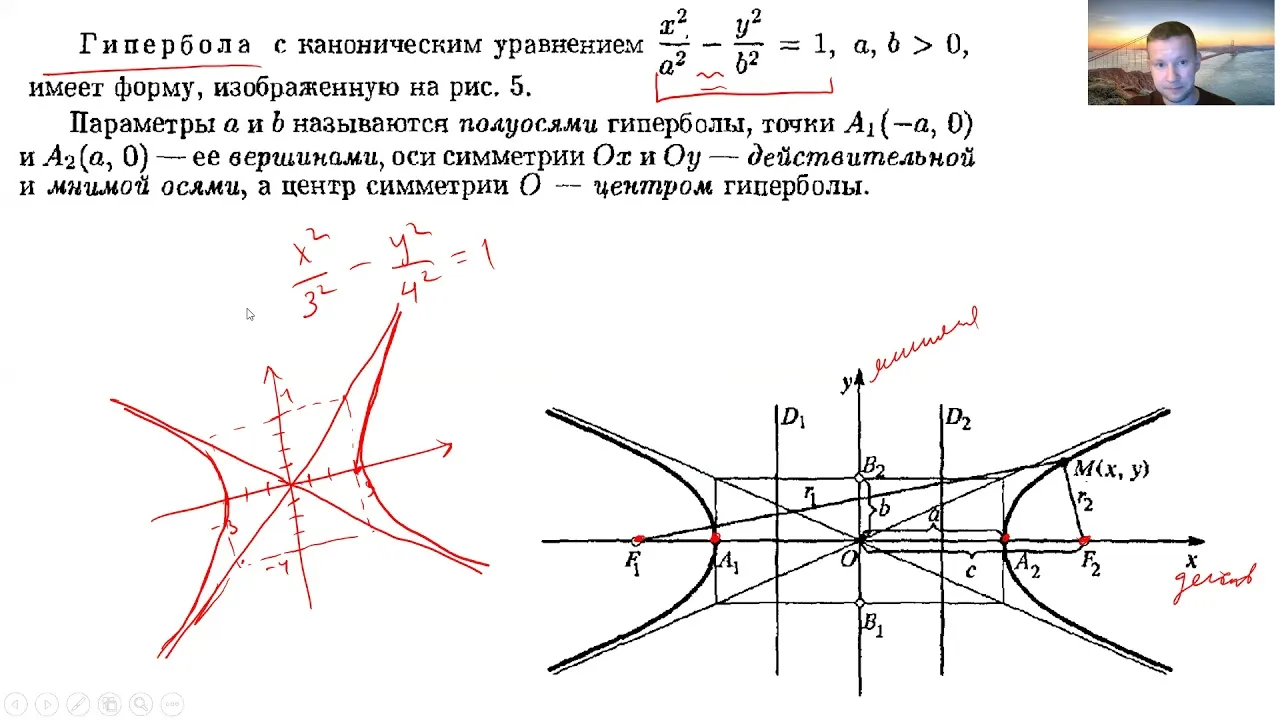
Гипербола - это кривая, определяемая как множество точек, для которых разность расстояний до двух фиксированных точек, называемых фокусами, постоянна. Фокусы гиперболы обозначаются буквами F₁ и F₂.
Уравнение гиперболы
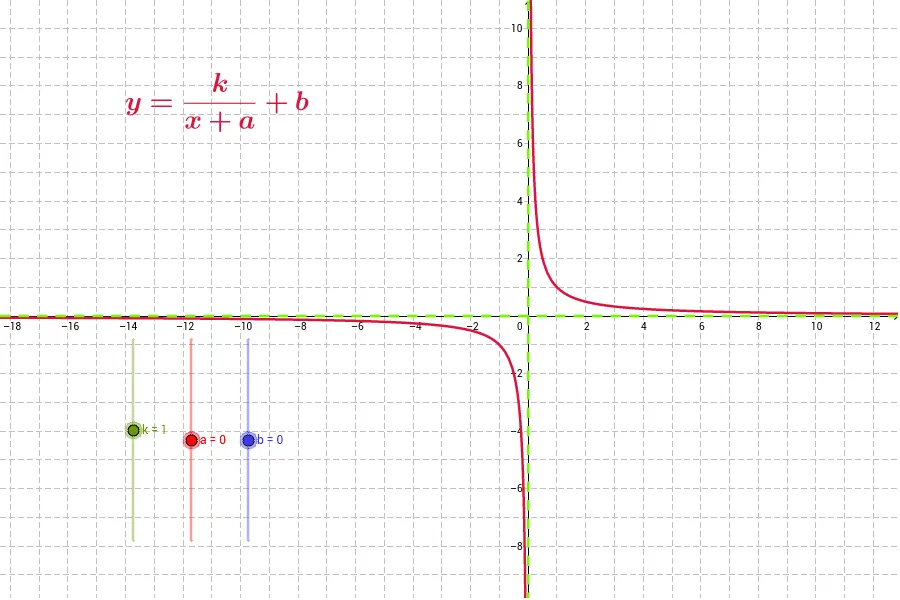
Уравнение гиперболы в общем виде имеет следующий вид:
x²/a² - y²/b² = 1
где a и b - полуоси гиперболы.
Основные характеристики гиперболы
Гипербола имеет несколько характеристик, которые определяют ее форму и свойства:
-
Фокусы: Гипербола всегда имеет два фокуса, которые находятся на главной оси гиперболы. Расстояние от любой точки гиперболы до каждого из фокусов постоянно.
-
Директрисы: Гипербола также имеет две директрисы, которые расположены на главной оси гиперболы. Директрисы определяются таким образом, чтобы расстояние от любой точки гиперболы до директрисы было постоянным.
-
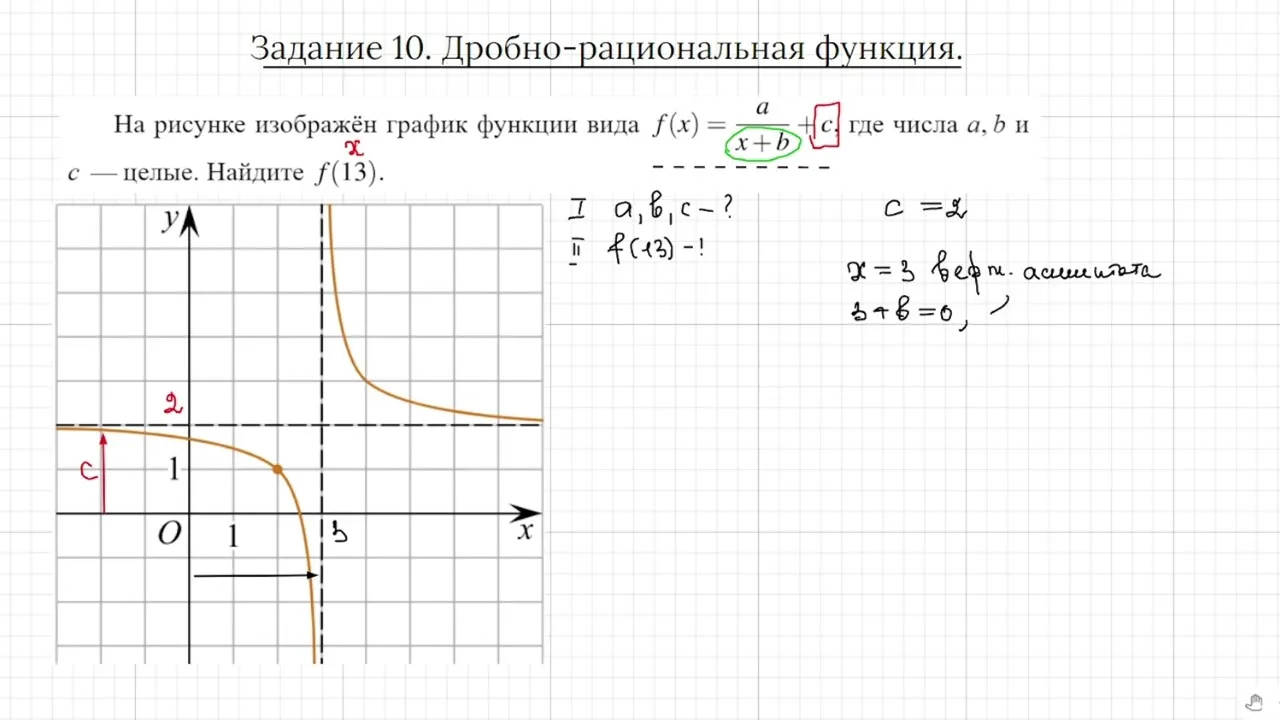
Асимптоты: Гипербола имеет две асимптоты, которые проходят через фокусы и пересекаются в центре гиперболы. Асимптоты определяют направление, в котором гипербола расширяется в бесконечность.
Применение гиперболы
Гипербола широко используется в различных областях, включая:
-
Математика: Гипербола играет важную роль в математическом анализе и геометрии. Она используется для моделирования различных процессов и явлений, таких как движение планет, электромагнитные поля и оптические системы.
-
Физика: Гипербола применяется в физике для описания траекторий движения объектов в гравитационных полях, электромагнитных полях и других физических системах.
-
Инженерия: Гипербола используется в инженерных расчетах и конструкциях, таких как антенны, зеркала и оптические системы. Форма гиперболы позволяет управлять фокусным расстоянием и свойствами лучей света или радиоволн.
-
Финансы: Гипербола также применяется в финансовой математике для анализа временных рядов и прогнозирования финансовых показателей.
Заключение
Гипербола - это кривая с уникальной формой, которая имеет множество применений в различных областях. Она играет важную роль в математике, физике, инженерии и финансах. Изучение гиперболы позволяет нам лучше понять мир вокруг нас и применять этот знаний для решения различных задач и проблем.

