




































Прямоугольник - это геометрическая фигура, которая имеет четыре стороны и четыре угла. У прямоугольника все углы равны 90 градусам. Это делает его особенно полезным и широко используемым в различных областях, таких как математика, инженерия, архитектура, графика и дизайн.
Прямоугольник имеет несколько ключевых характеристик:
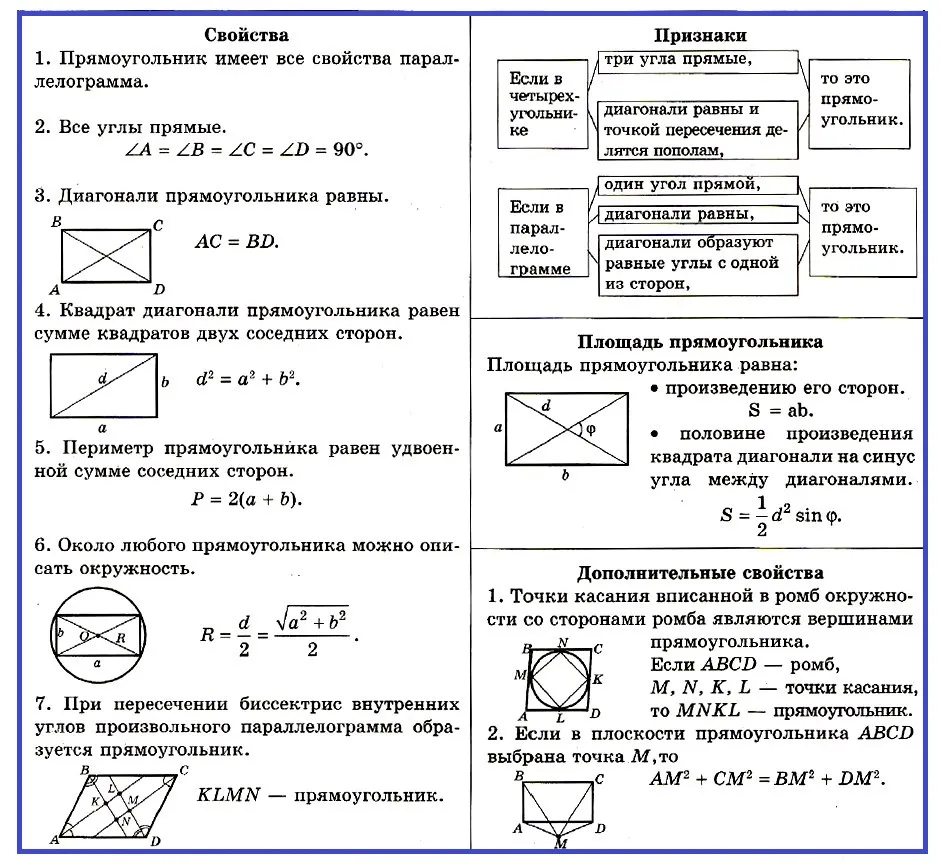
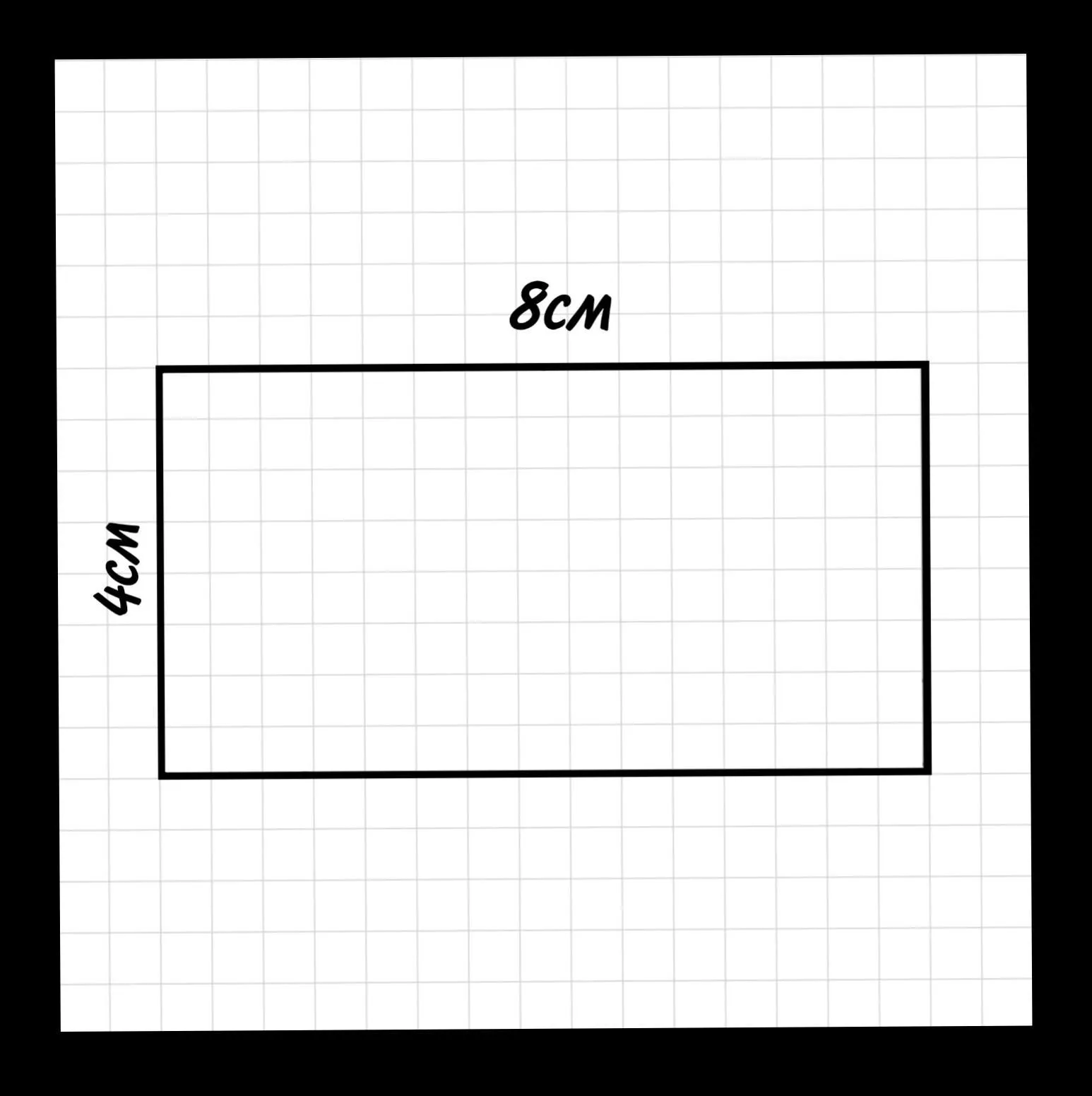
1. Длина и ширина: Прямоугольник определяется своей длиной (вертикальной стороной) и шириной (горизонтальной стороной). Эти две стороны могут быть разной длины, но они всегда пересекаются под прямым углом.
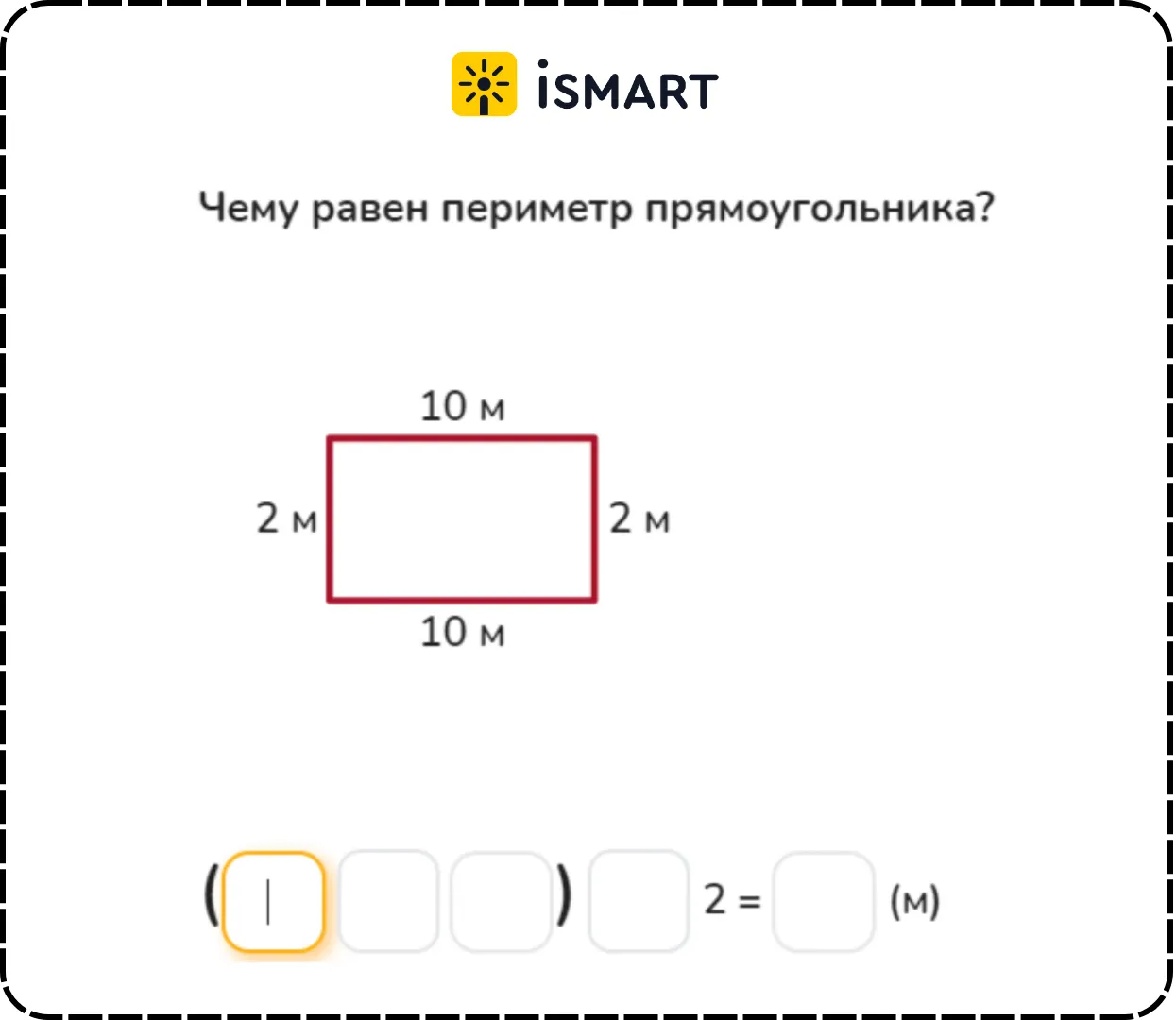
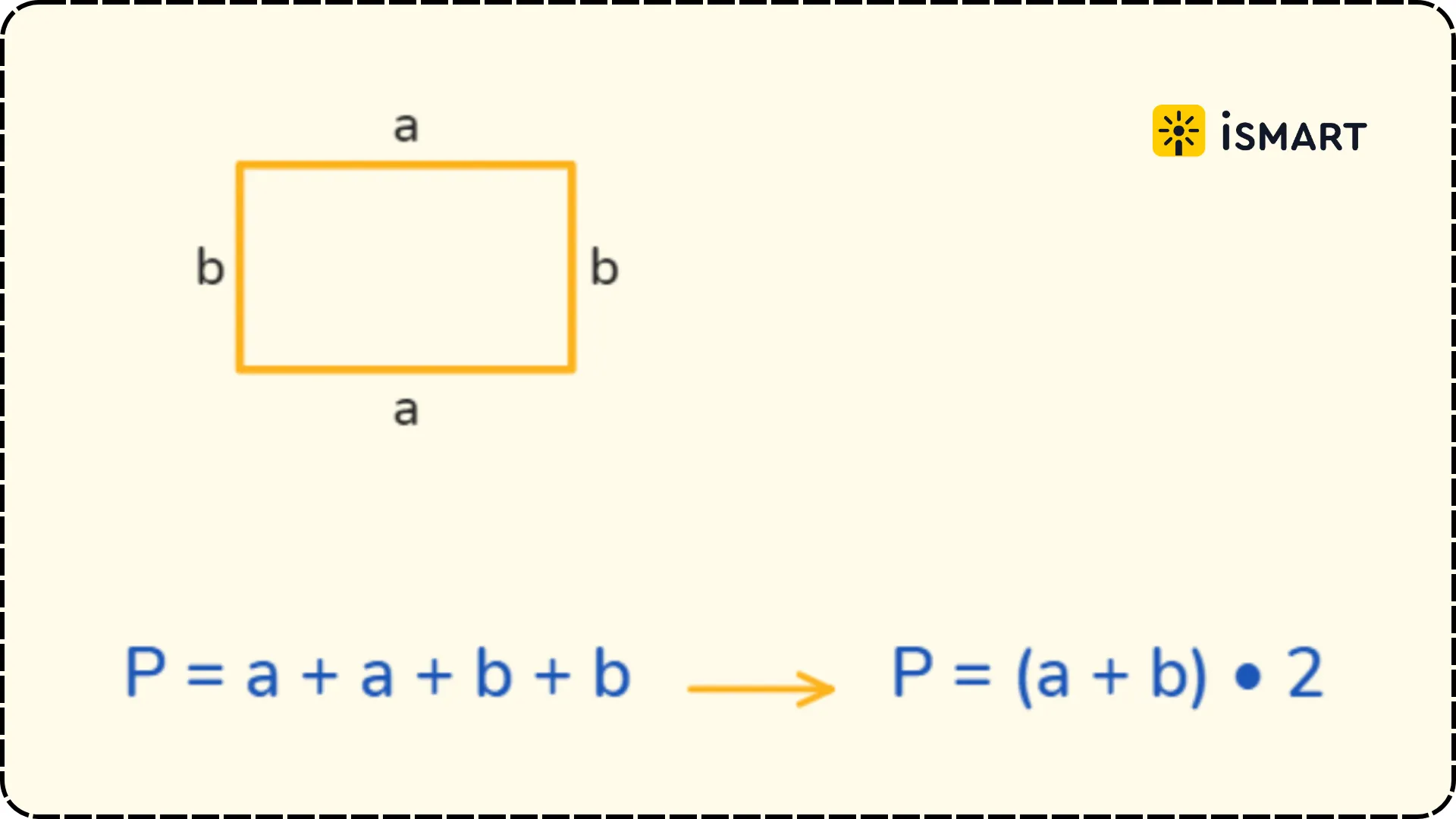
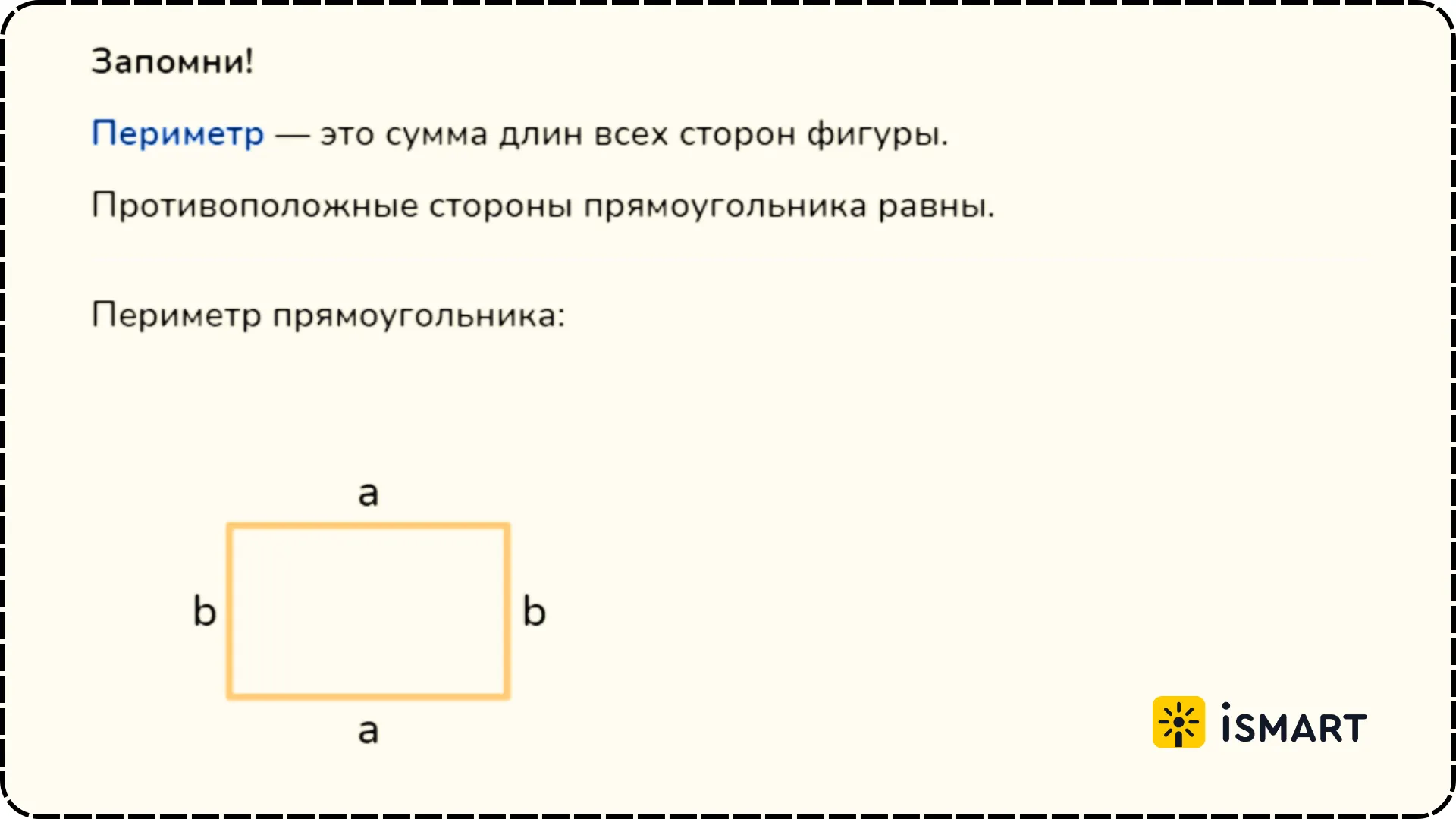
2. Периметр:
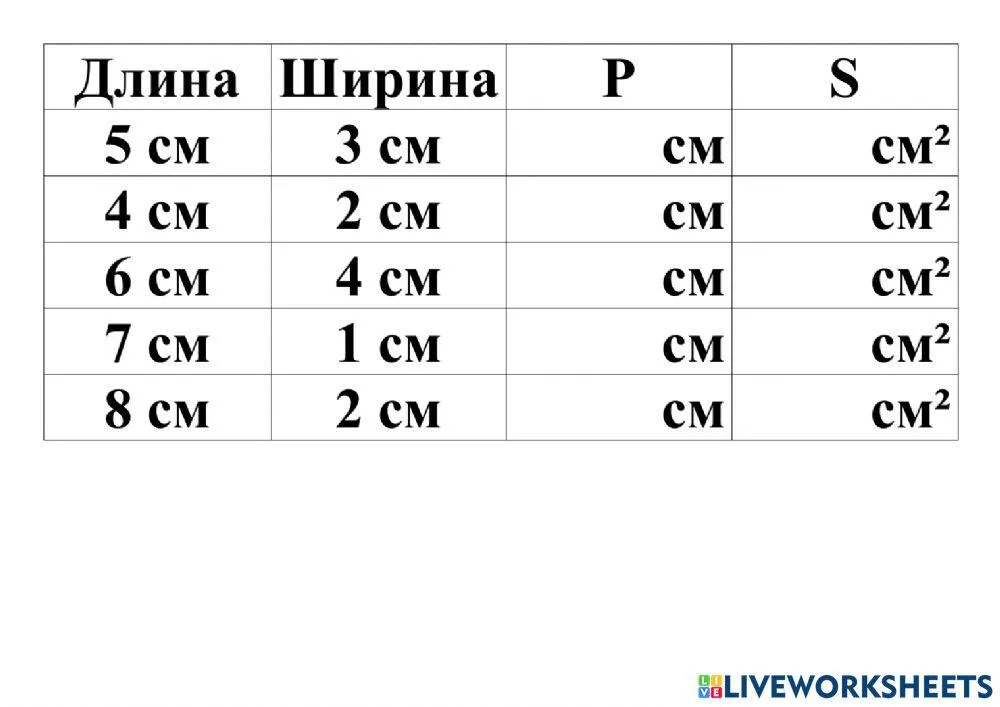
Периметр прямоугольника - это сумма длин всех его сторон. Он вычисляется по формуле: Периметр = 2 * (Длина + Ширина). Периметр прямоугольника показывает, сколько длины необходимо пройти, чтобы обойти его.
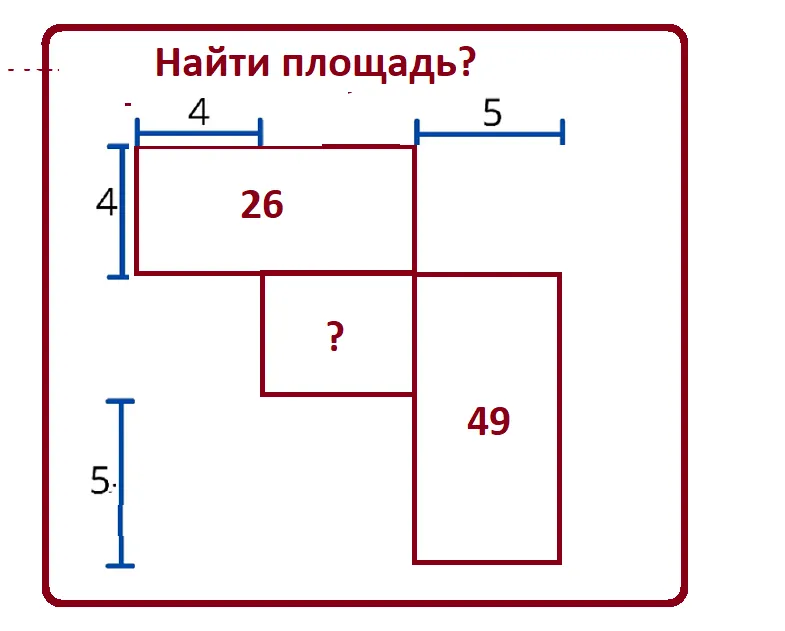
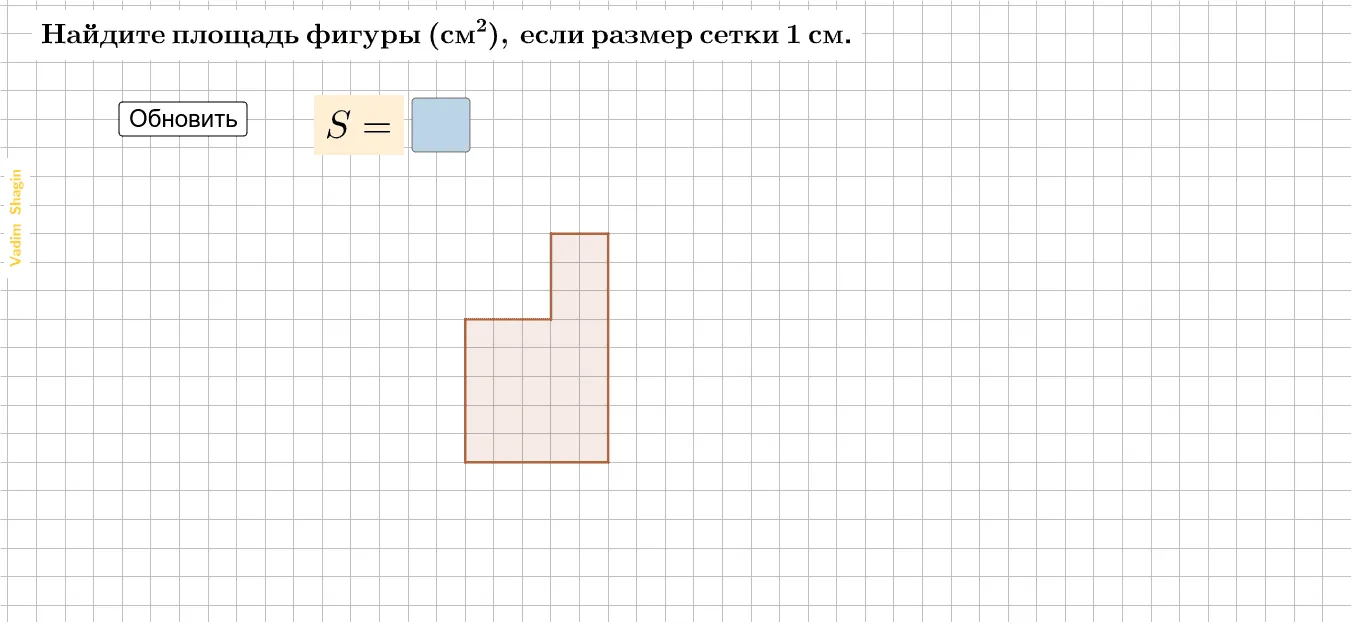
3. Площадь:
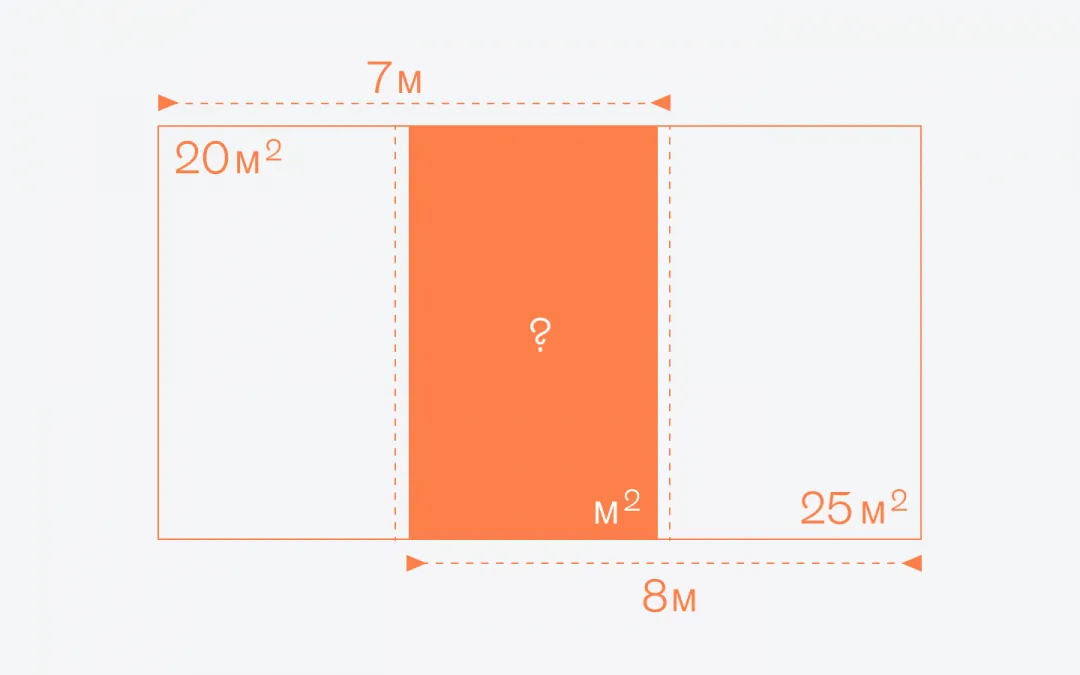
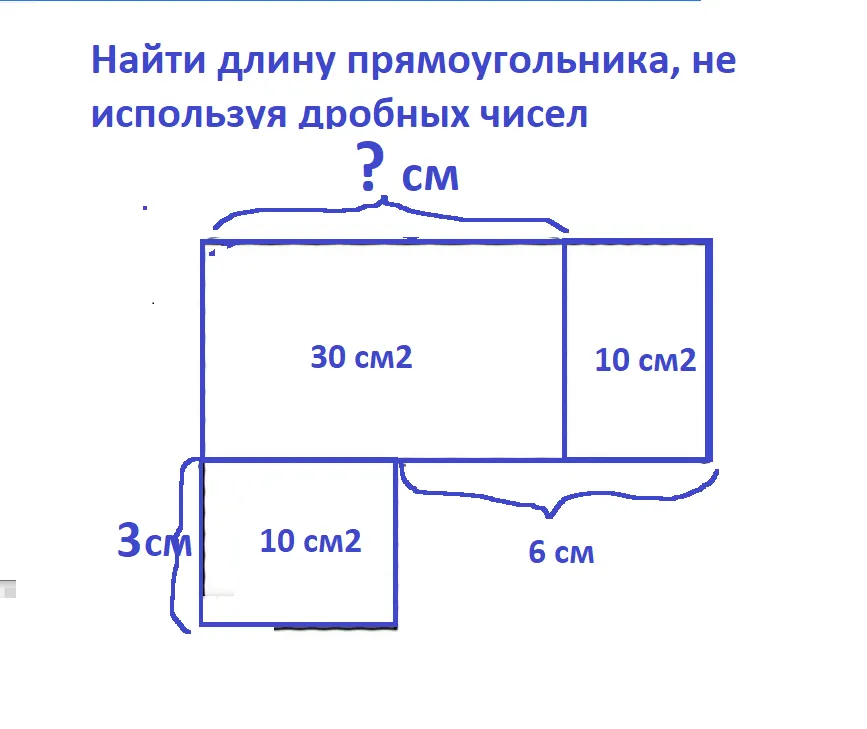
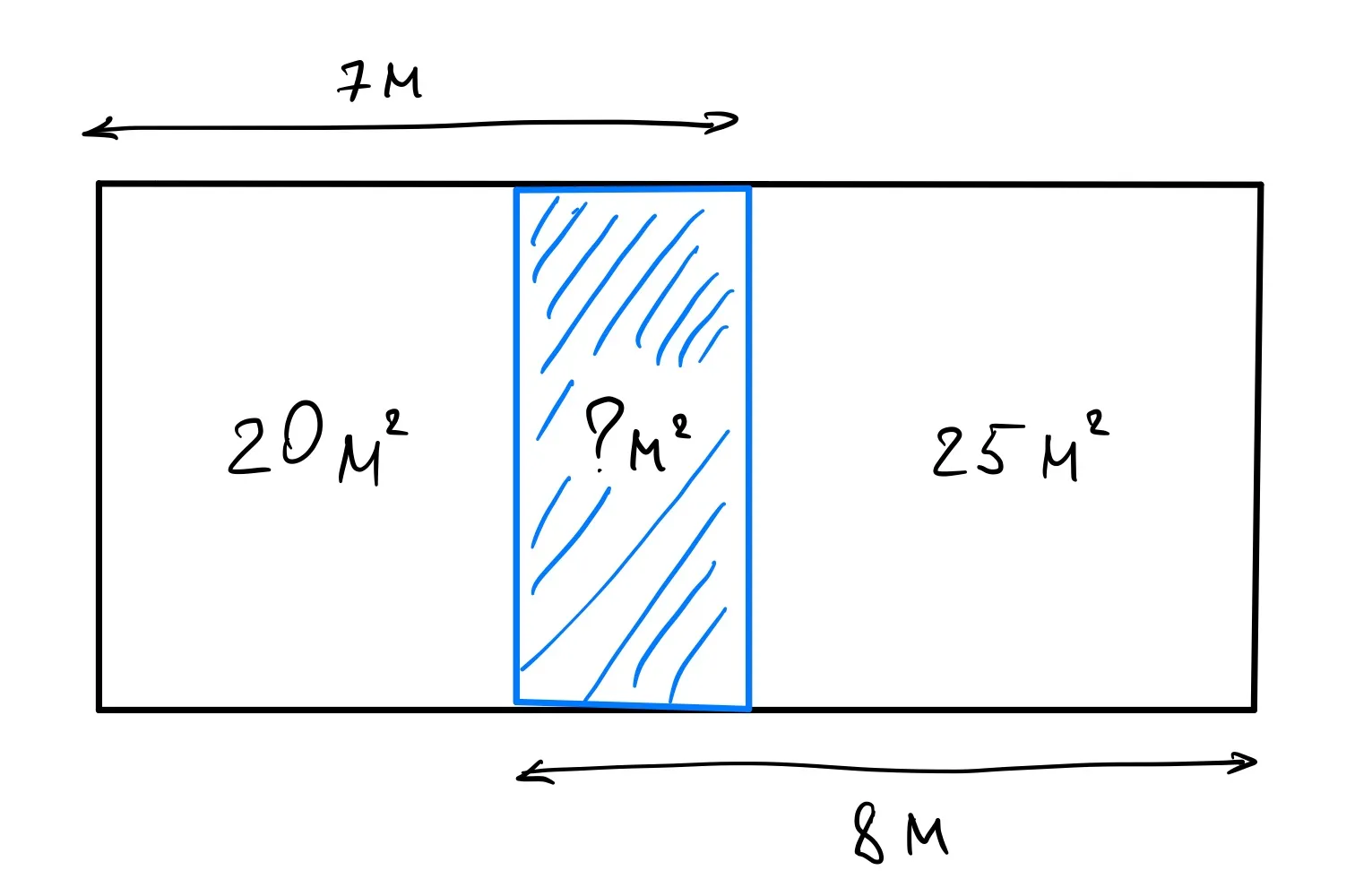
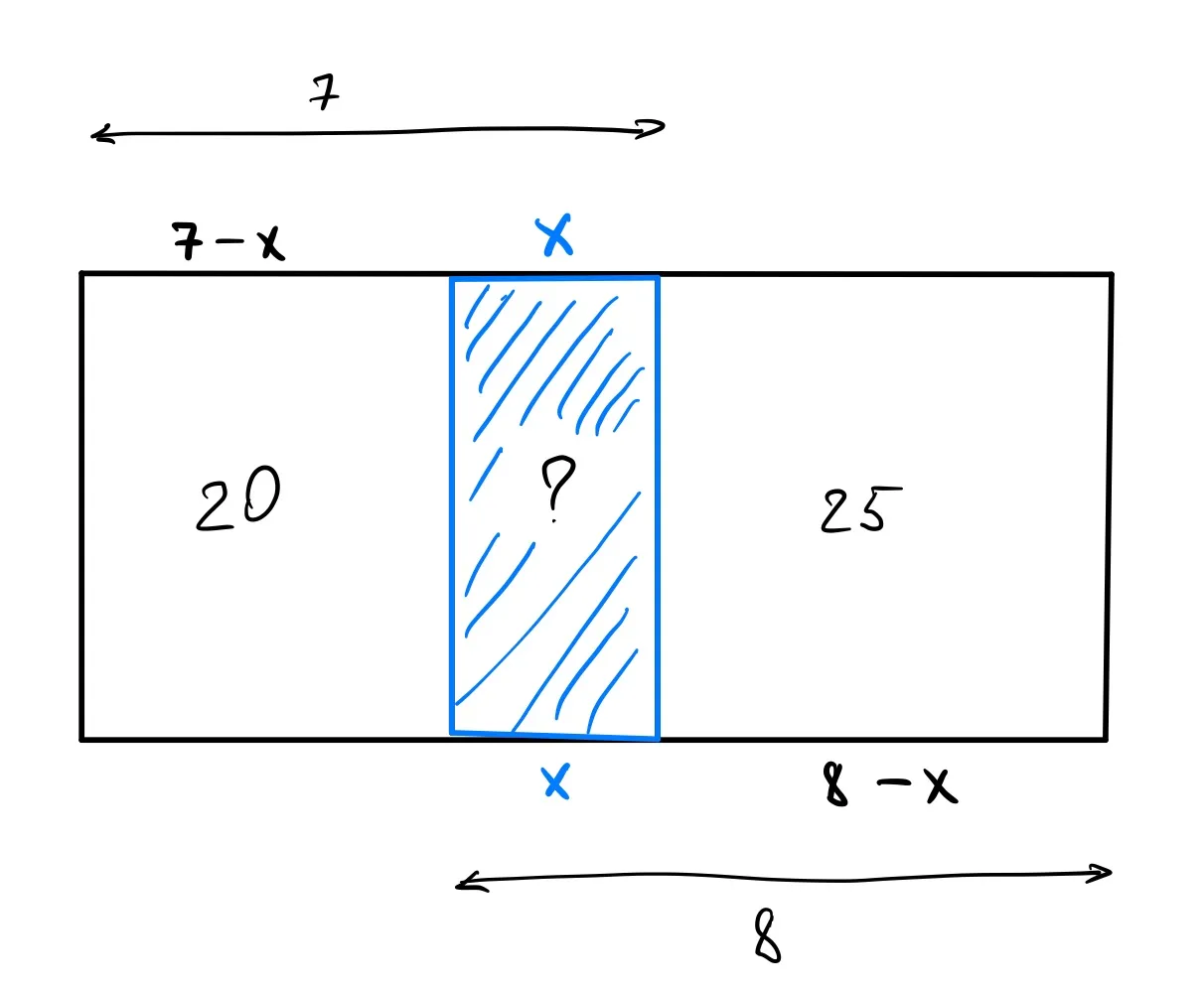
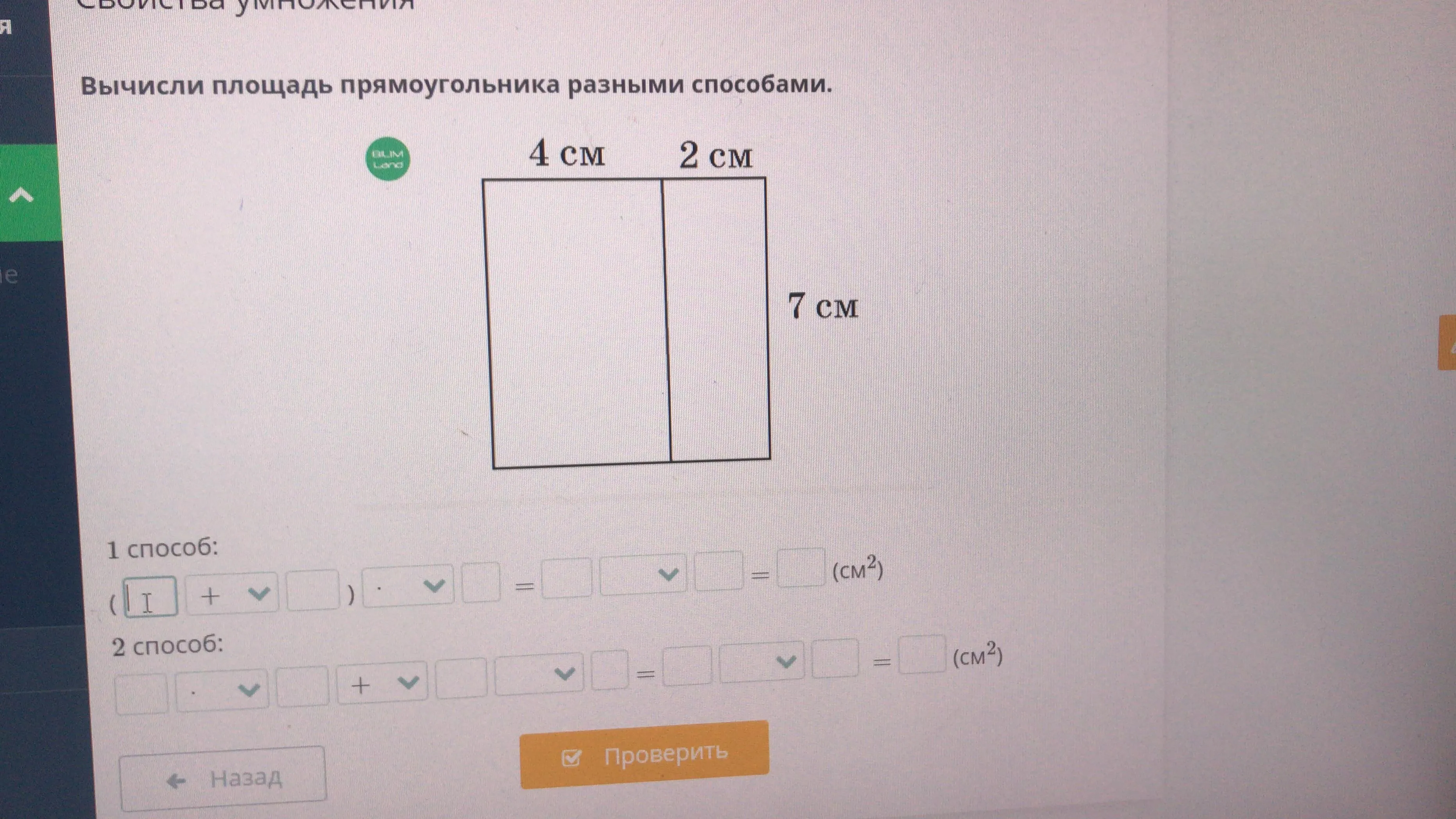
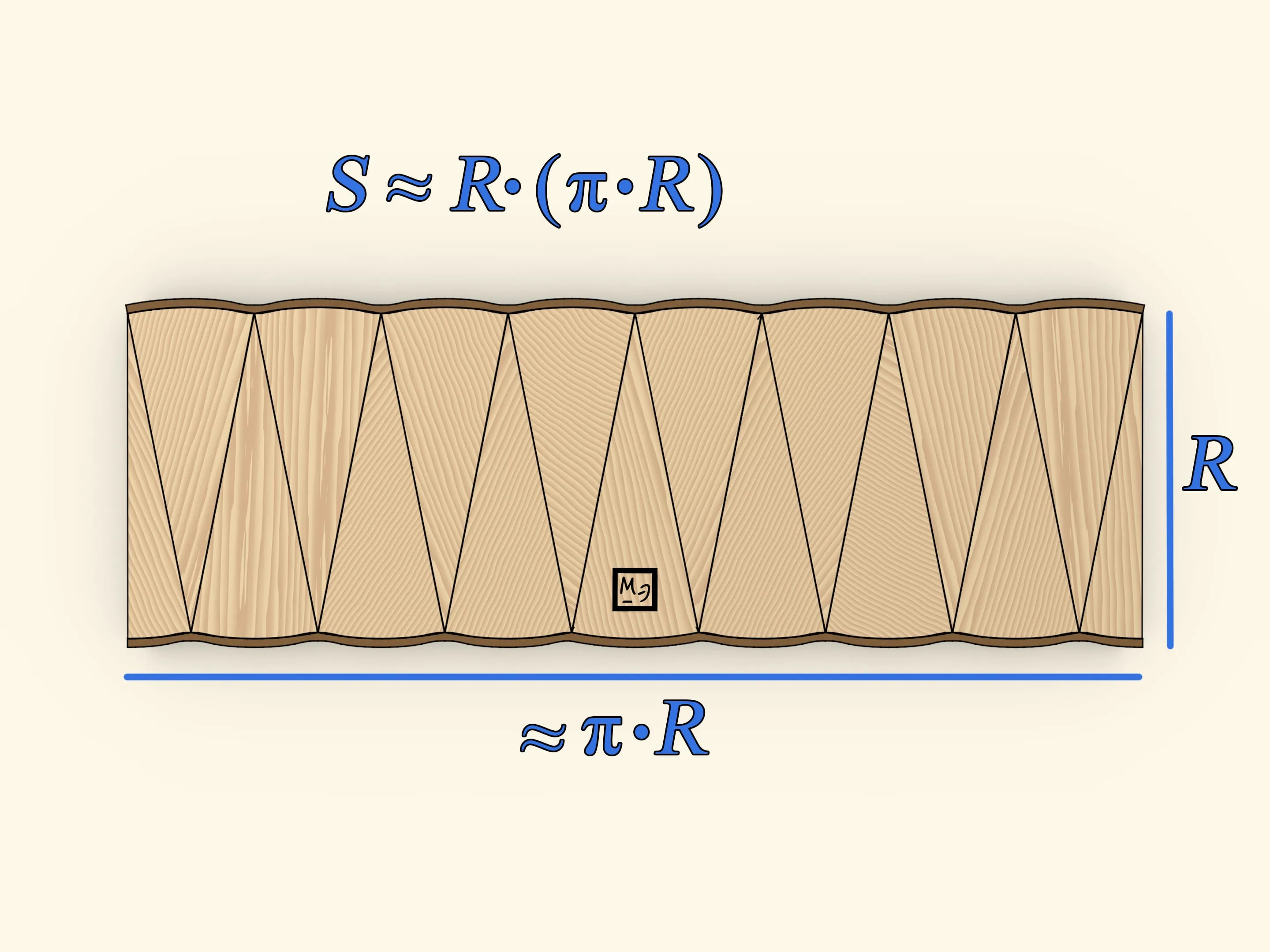
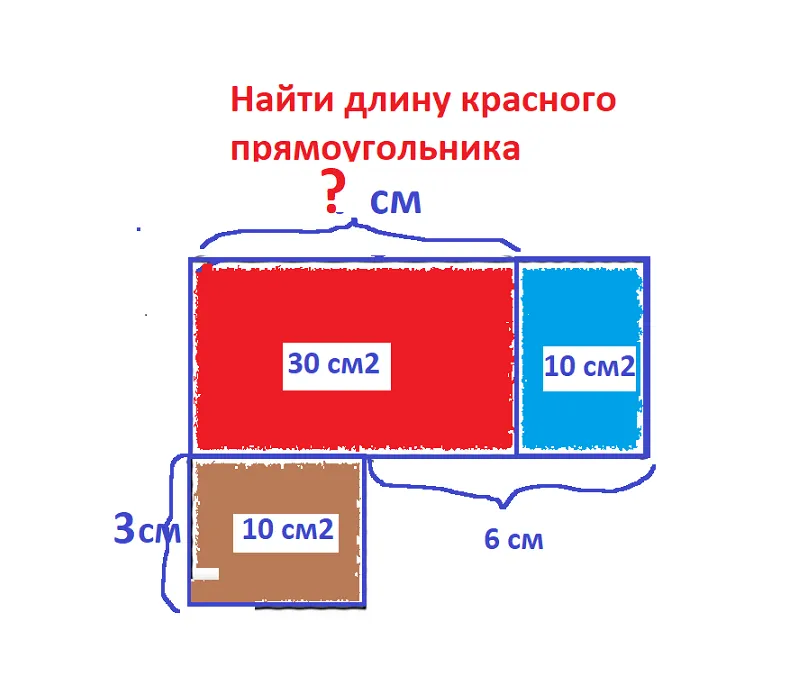
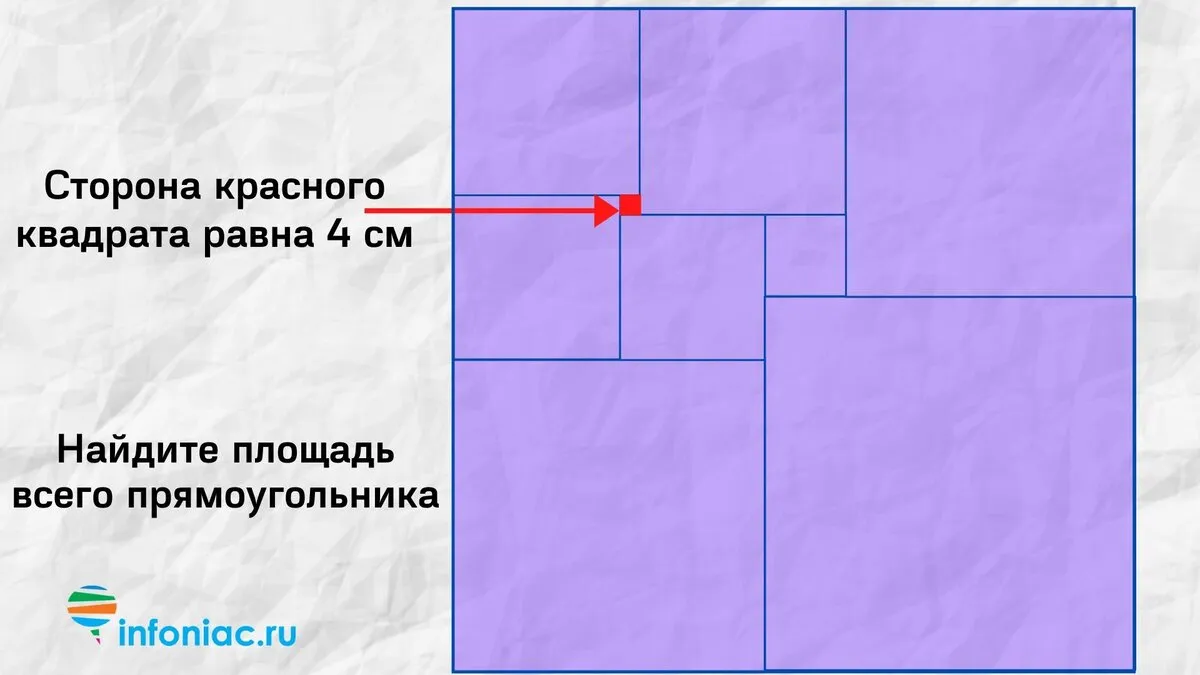
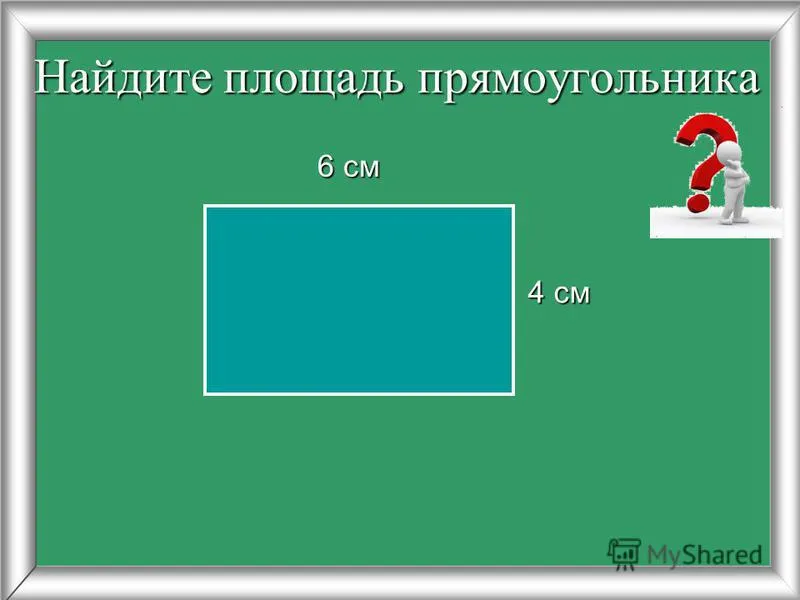
Площадь прямоугольника - это количество площади, заключенной внутри его границ. Его можно вычислить, умножив длину на ширину: Площадь = Длина * Ширина. Площадь прямоугольника измеряется в квадратных единицах (например, квадратных метрах или квадратных дюймах) и показывает, сколько места занимает прямоугольник на плоскости.
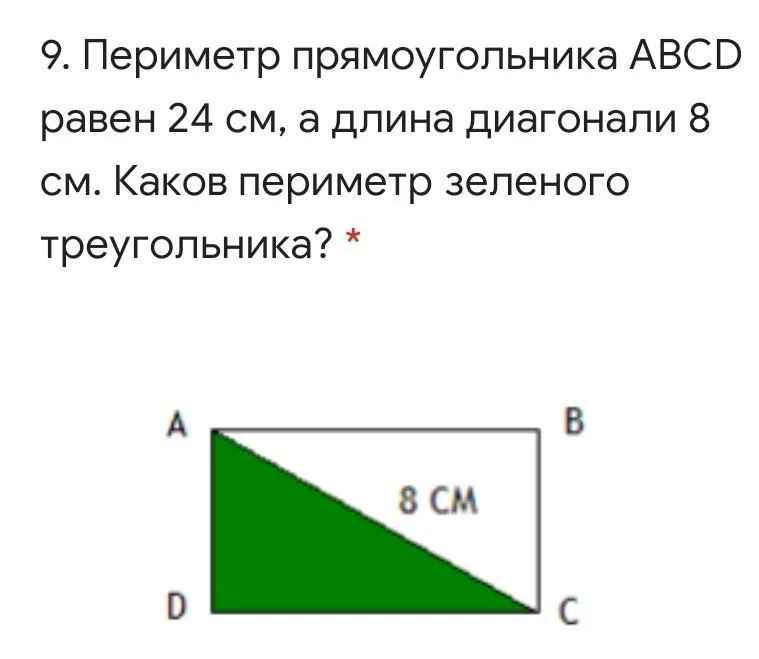
4. Диагональ:
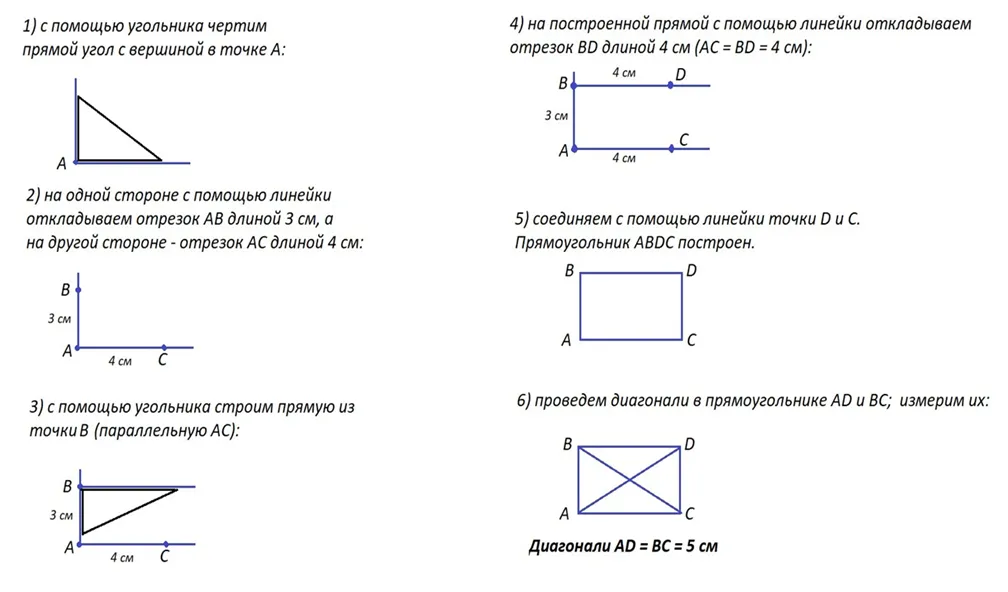
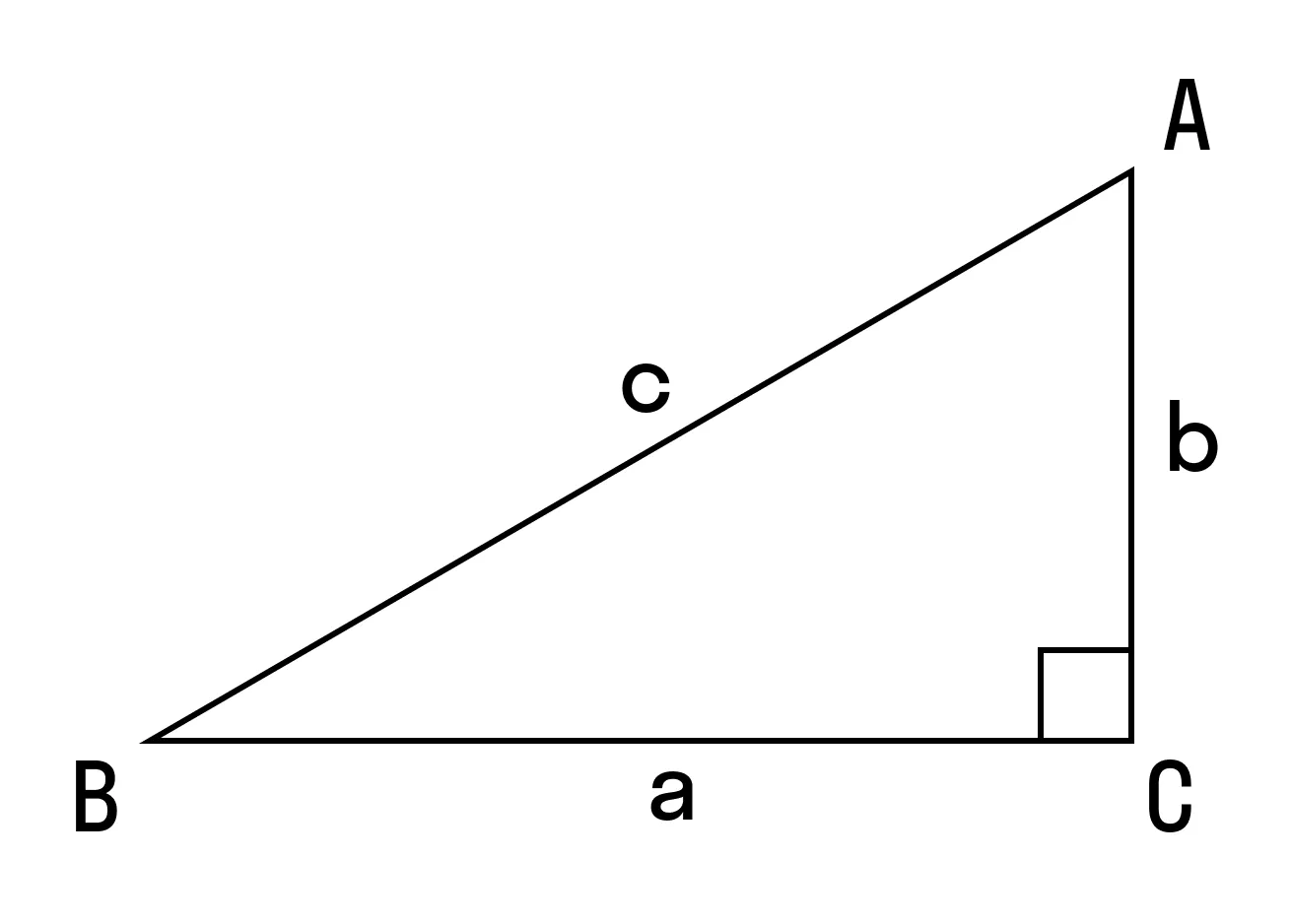
Диагональ прямоугольника - это отрезок, соединяющий две противоположные вершины. Его длина может быть вычислена по теореме Пифагора: Диагональ = √(Длина² + Ширина²). Диагональ прямоугольника может использоваться для измерения его диагонального расстояния или для определения максимальной длины отрезка, который можно нарисовать внутри прямоугольника.
Прямоугольники находят широкое применение в различных областях. Они могут быть использованы для строительства зданий, проектирования интерфейсов веб-страниц, создания графиков и диаграмм, разработки компьютерных игр и многого другого. Изучение прямоугольников и их свойств играет важную роль в математике и физике.
Благодаря своей простоте и универсальности, прямоугольник является одной из наиболее распространенных и полезных геометрических фигур. Он обладает множеством интересных свойств и может быть использован во многих задачах и приложениях.

